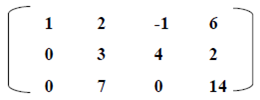Komputasi Proses (Sistem Persamaan Linear Metode Eliminasi Gauss Jordan)

Salah satu metode yang dapat digunakan untuk menyelesaikan sistem persamaan linier adalah metode eliminasi Gauss-Jordan. Metode ini diberi nama Gauss-Jordan untuk menghormati Carl Friedrich Gauss dan Wilhelm Jordan. Metode ini sebenarnya adalah modifikasi dari metode eliminasi Gauss, yang dijelaskan oleh Jordan di tahun 1887.

Metode Gauss-Jordan ini menghasilkan matriks dengan bentuk baris eselon yang tereduksi (reduced row echelon form), sementara eliminasi Gauss hanya menghasilkan matriks sampai pada bentuk baris eselon (row echelon form).

Selain untuk menyelesaikan sistem persamaan linier, metode eliminasi Gauss Jordan ini dapat pula digunakan untuk mencari invers dari sebuah matriks.

Prosedur umum untuk metode eliminasi Gauss-Jordan ini adalah :

1.      Ubah sistem persamaan linier yang ingin dihitung menjadi matriks augmentasi.

2.      Lakukan operasi baris elementer pada matriks augmentasi (A|b) untuk mengubah matriks A menjadi dalam bentuk baris eselon yang tereduksi.

Pengubahan dilakukan dengan membuat matriks yang elemen-elemennya adalah koefisien-koefisien dari sistem persamaan linier.

Sedangkan langkah-langkah pada operasi baris elementer yaitu,

1.      Menukar posisi dari 2 baris.

A_i ↔ A_j

2.      Mengalikan baris dengan sebuah bilangan skalar positif.

A_i = k * A_j

3.      Menambahkan baris dengan hasil kali skalar dengan baris lainnya.

A_i = A_i + k * A_j

Sebuah matriks sendiri bisa dikatakan sudah memiliki bentuk baris eselon yang tereduksi jika telah memenuhi syarat-syarat berikut ini.

1.    Jika sebuah baris seluruhnya bukan merupakan angka nol, maka angka bukan nol pertama pada baris tersebut adalah 1 (leading 1).

2.    Jika ada baris yang seluruhnya terdiri dari angka nol, maka baris tersebut dikelompokkan di baris paling bawah dari matriks.

3.    Jika ada 2 baris berurutan yang sama-sama tidak terdiri dari angka nol seluruhnya, maka leading 1 dari baris yang lebih bawah berada di sebelah kanan dari leading 1 yang berada di baris yang lebih atas.

4.    Pada setiap kolom yang memiliki leading 1 di kolomnya, maka nilai yang ada di kolom tersebut kecuali leading 1 adalah nol.

Sebuah matriks yang hanya memenuhi syarat 1 sampai 3 adalah matriks yang dalam bentuk baris eselon. Sedangkan jika syarat keempat juga dipenuhi, maka matriks tersebut dapat dikatakan dalam bentuk baris eselon yang tereduksi.

Berikut beberapa contoh matriks yang sudah dalam bentuk baris eselon tereduksi.

Berikut contoh langkah-langkah yang dilakukan untuk menyelesaikan system persamaan linier dengan metode eliminasi Gauss-Jordan.

Diketahui sistem persamaan linier sebagai berikut.

1.      Ubah sistem persamaan linier di atas menjadi matriks augmentasi.

2.   Kalikan baris pertama dengan 0.5

3.       Tambahkan baris kedua dengan (-1) kali baris pertama

4.      Tambahkan baris ketiga dengan 3 kali baris pertama

5.      Kalikan baris kedua dengan 1/3

                 

6.      Tambahkan baris pertama dengan (-2) kali baris kedua

7.      Tambahkan baris ketiga dengan (-7) kali baris kedua

                    

8.      Kalikan baris ketiga dengan -1/9.33

9.      Menambahkan baris pertama dengan 3.67 kali baris ketiga

10.   Menambahkan baris kedua dengan (-0.33) kali baris ketiga

Setelah langkah ke-10, maka matriks ini telah dalam bentuk baris eselon tereduksi. Dari matriks terakhir ini dapat disimpulkan bahwa nilai x = 1, y = 2, dan z = -1.

Contoh di atas diterapkan pada sistem persamaan linier dengan n variabel dan n persamaan.

Contoh berikut adalah cara menyelesaikan sistem persamaan linier dengan n variabel dan m persamaan.

Diketahui sistem persamaan linier sebagai berikut.

Penyelesaian untuk persamaan di atas akan menjadi

Ada 3 macam kemungkinan penyelesaian dari sistem persamaan linier, yaitu :

1.      Solusi yang unik. Hanya ada satu himpunan nilai (s1, s2, ..., sn) yang memenuhi system persamaan linier tersebut.

2.      Tidak ada solusi. Tidak ada himpunan nilai (s1, s2, ..., sn) yang memenuhi system persamaan linier tersebut.

Solusi yang ada tidak berhingga. Ada lebih dari satu (tak berhingga) himpunan nilai (s1, s2, ..., sn) yang memenuhi sistem persamaan linier tersebut

referensi :

Senjaya Johan, 2011. Komputasi Proses. Teknik Kimia USU.